자바스크립트로 배우는 SICP - 10. 그림 언어와 데이터 추상화

그림으로 알아보는 추상화! (잠시 쉬어가는 코너...?)

2023-11-02 | 독서 | 12min

오늘은 그림 언어를 통해 데이터 추상화와 닫힘 성질을 활용하는 예시에 대해서 읽었다!

이번 부분의 메인 키워드는 다음과 같다!

키워드

• 그림 언어
• 화가 요소
• 조합 패턴의 추상화
• 액자 객체
• 화가 요소와 추상화 장벽

이 파트에 대한 나의 생각

이번 내용은 하나의 예시 파트로서 데이터 추상화의 힘을 보여주는 파트라고 생각한다. 내 생각에는 이전까지 다루던 데이터는 추상화가 진행되면 진행될수록 그 원시 형태를 보여주지 않는 블랙박스로서의 성질이 강력해져 점점 추상화 사실에 대해 무감각해지는 것을 보완하기 위해서 만들어진 부분이 아닐까 싶다.

그림 언어

우선 저자는 그림 언어 를 소개한다. 이는 단순히 자바스크립트 를 대체하는 언어라고 생각하자!

자바스크립트에는 여러가지 원시적 요소들이 존재하지만, 저자가 소개하는 그림 언어에는 요소가 화가 요소 한 가지만 존재한다. 이는 단순히 말하면 하나의 그림이다! (당연하다… 그림 언어니깐..?)

그림 언어는 액자 에 들이맞게 기울여지거나 확대 및 축소가 이루어진 하나의 이미지를 의미한다.

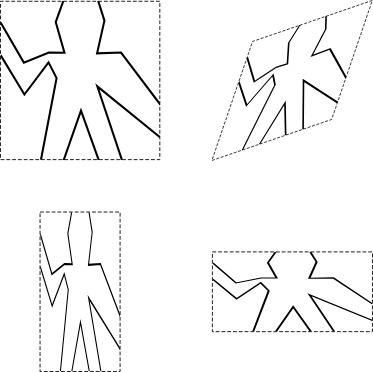
위와 같은 그림을 보자! 네 가지 그림들은 모두 같은 화가 요소 를 지닌다. 이를 우리가 흔히 말하는 하나의 이미지 라고 생각해도 무방하다. 대신 차이점은 같은 이미지를 담는 액자가 달라진 것이다.

그림 언어의 조합

이제 그림 언어들을 조합해보자! 여러 화가 요소들을 이어 붙이면 또 다른 형태의 이미지를 만들 수 있을 것이다!

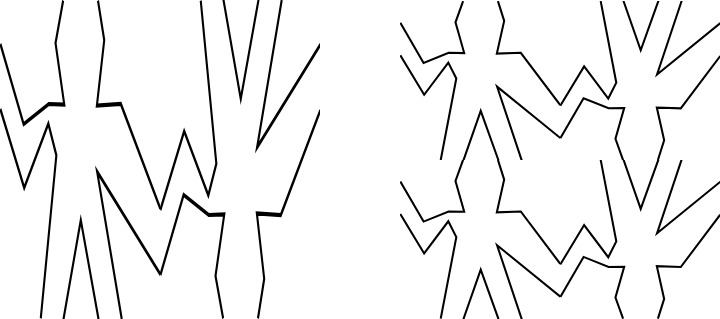
위 두 그림은 앞서 본 화가 요소 를 뒤집거나 이어 붙여서 만들어진 복합 화가 요소라고 할 수 있다.

이를 코드로 표현해보자!

const img_1 = beside(img, flip(img)); // 왼쪽 요소이다!
const img_2 = below(img_1, img_1); // 오른쪽 요소이다!

왼쪽 요소에 대한 코드는 flip 을 통해 기존의 화가요소를 뒤집고, beside 를 이용하여 두 화가 요소들을 이어 붙이고 있다. 이렇게 만들어진 복합 요소인 img_1 를 below 라는 함수를 이용하여 아래로 붙여 또 다른 하나의 복합 화가 요소를 만들어 내고 있다.

이 예시에서 강조하고 있는 부분이 바로 닫힘 성질 이다! 화가 요소들을 조합하여 또 다른 화가 요소 들을 만들어내고 있으니, 이는 대수학에서 다루는 “닫혀있다” 라는 개념을 활용하면, 데이터가 조합 수단에 대해 닫혀있다는 성질임을 보여주고 있다는 것이다. (애초에 데이터가 닫힘 성질을 지녀야만 조합을 통해 복합 요소를 만들어 낼 수 있다!)

복합 요소들에서의 추상화

앞서 다뤘던 img_2 는 이를 하나의 함수로 바꿀 수 있다.

function flipped_pairs (img) {
	const img_1 = beside(img, flip(img));
	return below(img_1, img_1)
}
 
const img_2 = flipped_pairs(img_1)

다른 예시를 보자! 아래의 두 그림을 코드로 구현해보자.

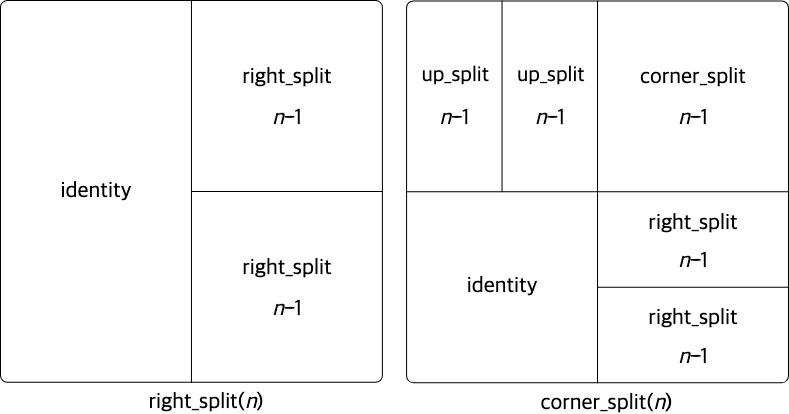
right_split 은 어떻게 구현할까? (애초에 n번째의 형태를 n-1번째의 형태로 표시하는 것을 보면 점화식 형태라 재귀적 함수로 작성 가능하겠다는 예측이 가능할 것이다.)

• 우선 하나의 화가 요소가 위 아래로 붙여진 형태가 필요할 것이다.
• 그리고 이는 초기 화가 요소의 오른쪽에 이어져 있을 것이다.
• 위 과정을 반복해서 n번 동안 오른쪽으로 분할되는 과정을 거칠 것이다. 이는 재귀적으로 구현하면 될 것이다.

자 그럼 코드를 보자! 참고로 화가 요소를 이제부터 painter 이라고 하겠다!

function right_split(painter, n) {
    if (n === 0) {
        return painter;
    } else {
        const smaller = right_split(painter, n - 1);
        return beside(painter, stack(smaller, smaller));
    }
}

간단한 코드이다! n이 0이라면, 단순히 기존의 화가 요소를 반환하면 된다. 만약 아니라면, 그림이 보여주듯 점화식으로 표현하면 된다! smaller 라는 n-1번째 요소를 선언하여 이를 이용하여 stack 을 구성하고 beside 로 이어붙여주면 된다. (사실 식만 다를 뿐이지 $f(n) = p + f(n-1)$ 와 다를 바가 없는 구조이다. 연산이 자바스크립트의 원시적 요소인 + 이 아니기에 함수로 대체했을 뿐.)

그럼 corner_split 은 어떻게 구현할까? 똑같다!

function corner_split(painter, n) {
    if (n === 0) {
        return painter;
    } else {
        const up = up_split(painter, n - 1);
        const right = right_split(painter, n - 1);
        const top_left = beside(up, up);
        const bottom_right = stack(right, right);
        const corner = corner_split(painter, n - 1);
        return stack(beside(top_left, corner),
                     beside(painter, bottom_right));
    }
}

보기 쉽게 수학 식으로 표현해보면 다음과 같다.

그리고 각 + 요소들을 그림에 따라 beside 또는 stack 으로 이어 붙여주면 완성되는 코드이다!

조합 패턴의 추상화

그럼 조합되는 패턴을 추상화 할 수 있을까? 앞서 다뤘던 flipped_pair 을 보면, beside 와 below 의 조합으로 이루어져 있다. 하지만 이를 달리보아 액자를 사분면으로 나누어 각 사분면에 어떤 화가 요소들이 들어갈지 결정할 수 있는 함수를 만든다면 어떨까?

function square_of_four(tl, tr, bl, br) {
    return painter => stack(beside(tl(painter), tr(painter)),beside(bl(painter), br(painter)));
}

위 코드와 같이 구현할 수 있을 것이다! 각 사분면의 요소들을 받아서 각 요소들을 beside 와 stack 으로 이어주는 함수이다! 이렇게 구현된 함수는 4등분하는 사분면의 형태를 가진 어떤 화가 요소들도 조합하는데 이용할 수 있는 고차 연산 에 속하게 된 것이다! (사실 자바스크립트로 보면 + 연산 4번을 하나의 함수로 추상화했다는 의미이다! 물론 이 그림 언어의 세계 속에서는 방향이 존재하기에 단순한 + 의 반복 적용이라고 하기엔 어렵지만…)

그럼 앞서 구현했던 flipped_pair 를 다시 구현하면 다음과 같을 것이다.

function flipped_pairs(painter) {
    const combine4 = square_of_four(turn_upside_down, flip_vert, flip_horiz, identity);
    return combine4(painter);
}

그냥 화가 요소들을 받은 뒤, 뒤집거나 동일한 요소들이 들어갈 자리를 배치해주면 완성이다!

액자 객체

지금까지는 화가 요소들의 조합에 집중했다. 여기서 한 가지 짚고 넘어가야되는 점은 앞서 다뤘던 그림 언어를 이루는 요소들에는 화가 요소 하나가 있었다는 것이 기억날 것이다. 하지만, 같은 화가 요소더라도 이 요소를 담는 그릇이 바뀔 수 있다는 것에 주의를 해야 한다. 이는 곧 언급했듯 액자 또는 프레임이다.

하지만, 그림의 틀 또는 액자 또는 액자 객체는 언제나 변경될 수 있다. 그렇다면 이를 일반화할 수는 없을까?

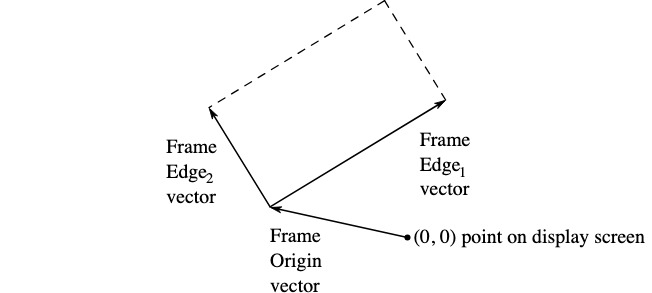
위 그림을 기반으로 벡터는 다음과 같이 표현할 수 있다.

이제 위 등식을(하나의 벡터를) 만드는 함수를 작성해보자.

function frame_coord_map(frame) {
	return v => add_vect(origin_frame(frame),
                add_vect(scale_vect(xcor_vect(v), edge1_frame(frame)),
                         scale_vect(ycor_vect(v), edge2_frame(frame))));
}

조금 함수가 복잡해 보일 수 있을 것이다. 하지만 당황하지 말자! 결국 앞서 그림 언어에서 다뤘듯 + 의 개념이 함수 add_vect 로 전환되었다는 점을 염두해두면 그리 어렵지 않은 함수이다.

어라? 그럼 위 함수는 어떤 역할을 하는 함수일까?

잘 보면,

• frame_coord_map 함수는 frame 을 매개 변수로 받는다. 그리고 이를 통해 원점으로 부터의 벡터 성분인 origin_frame 과 단위 벡터들인 edge1_frame , edge2_frame 를 확인한다.
• frame_coord_map 함수는 함수를 반환하고 있다. 그리고 이 함수는 하나의 인수를 받아 해당 인수의 단위 벡테의 배수를 확인하는데 이용된다.

그럼 이를 통해 어떤 것들이 가능할까?

frame_coord_map(a_frame)(make_vect(0,0))

위 코드는 어떤 것을 의미할까? 분석하면, “a_frame 의 틀 구조를 사용하되, 각 단위 벡터의 배수는 0이다.” 즉, 단순하게 원점으로부터 a_frame 의 벡터를 확인하고 있는 식이다. 그렇다면 아래와 동치일 것이다.

origin_frame(a_frame)

이처럼 origin과 두 단위 벡터에 대한 정보를 얻는다면, 액자의 벡터 좌표계는 정해지며 각 성분별 배수가 정해지는 즉시 액자 객체를 선언할 수 있게 된 것이다.

화가 요소를 구현하다..?

지금까지, 화가 요소들을 조합하는 연산의 추상화에 대해서 여러 예시들을 알아보았다. 그렇다면 화가 요소 자체가 과연 최소 단위의 요소일까? 그건 아닐 것이다. 왜냐하면 결국 화가 요소들도 점과 선으로 이루어져 있기 때문이다.

그렇다면 화가 요소들을 어떻게 구현할까? 가장 기본적인 요소는 선을 그리는 것이다. 이를 코드로 보면 다음과 같다.

function segments_to_painter(segment_list) {
	return frame => for_each(segment => draw_line(
                                          frame_coord_map(frame)(start_segment(segment)),
                                          frame_coord_map(frame)(end_segment(segment))),
                                          segment_list
                                        );
}

잘 살펴보자… 결론부터 말하자면, 이 함수는 선분에 대한 목록(또는 좌표 정보)을 받아 이를 좌표계에 그려 각 선분들을 화가 요소, 즉 이미지로 그린다.

• 우선 그리기 위한 선분 정보들을 포함한 segment_list 를 매개 변수로 받는다. 이는 곧 선분들의 좌표들에 해당할 것이다. (직교 좌표계의 좌표들일 것이다.) 이를 순회하면서 각 선분의 start_segment(시작점)과 end_segment(끝점)을 추출한다.
• 각 점들을 frame_coord_map 함수를 이용하여 벡터들을 만들어 낸다.
• 만들어진 시작점과 끝점으로의 벡터들을 draw_line 함수를 이용하여 선분을 그린다.
• 이 과정을 선분 리스트의 요소들에 대해서 반복한다.

어떻게 보면, 우리가 함수를 호출할 때 들어있는 점에 대한 정보를 → 벡터의 형태로 변환하고 → 이를 화가 요소 즉, 이미지로 화면에 표시하는 과정이 속해있다고 보면 된다.

이렇게 화가 요소를 그리는 방법에 대해서 알아보았다!

추상화 장벽?

과정이 길었지만, 크게 보면 앞선 내용들은 두 부분으로 나뉜다. 화가 요소를 활용하는 부분을 먼저 논했고, 화가 요소들을 구현하기 위한 부분을 이후에 논했다. 여기서 뭔가 느껴지지 않나…?

사실 두 부분에 대해서 얘기할 때, 서로 어떤 부분도 침범하지 않았다. 다시 말해, 화가 요소를 활용할 때 화가 요소가 어떻게 구현되어 있는지에 대해서 신경쓰지 않았다. 이는 곧 화가 요소 가 그림 언어에서의 강력한 추상화 장벽을 형성한다는 의미이다!

이제 화가 요소라는 추상적인 개념을 다시 조합하여 더욱 복합적인 요소들을 만들어나갈 수 있게 된 것이다. 그리고 이는 우리가 이전에 다뤘던 것이다!

사실 책에는 화가 요소들을 뒤집거나 변형하는 함수들에 대한 더 많은 예시들이 있지만, 결국은 화가 데이터의 추상화로 (즉, 화가 요소의 구현으로) 각 요소들 간 연산을 손쉽게 구현할 수 있다는 말을 하고 있다!

마무리

사실 이 파트는 간이역 느낌이었다. 데이터, 복합 데이터, 데이터 객체, 추상화 장벽 등의 많았던 생소한 단어들에 대한 개념을 시각화해서 이해하는데 편하라고 제시해준 예시이랄까? 그런 느낌이 많이 들었다. 그리고 꽤 많은 도움을 받았다. 특히 추상화 장벽을 이해하는데 도움이 많이 되었다.

음음 오늘도 알차구만! 그럼 다음으로 가보자!