자바스크립트로 배우는 SICP - 11. 데이터를 이용한 추상화 - 미분 편
이제는 미분이다! 추상화를 해보자 ~
2023-11-03 | 독서 | 5min
오늘은 이전의 유리수에 대한 추상화의 글에서 하였듯 도함수를 추상화해보는 내용을 읽었다! 전반적인 흐름은 유리수와 비슷하다. 결국은 추상화를 진행하기 위해서는 도함수가 적용될 수 있는 대수 시스템을 구축해야 하며 이를 위한 원시적 요소는 유리수에서는 수치에 제한적이지만 이제는 변수가 도입되게 된다.
변수와 상수의 곱, 합 등으로 이루어진 대수식을 표현하는 것도 문제이지만, 반대로 주어진 대수 식에서 역으로 변수, 상수, 곱, 합 등의 요소들을 꺼내올 수 있어야 한다.
예상했겠지만, 이 요소들에 대한 선택자를 바로 유리수에서 쌍 자료구조를 이용했듯 여기에서는 리스트 자료구조를 이용한다. 즉, 리스트 자료구조로 구현하면 선택자로 head 와 tail 함수가 유용하기 때문이다. 그렇다면 요소들의 조합을 어떻게 표시할까? 다시 말해, 생성자를 어떻게 표시할까?
이는 전위 표기법 을 이용하면 된다. 보통 우리가 수학에서 식을 쓸 때, x + y 는 중위 표기법 에 해당한다. 전위 표기법은 피연산자(연산 대상)들에 어떤 연산을 진행할지에 대한 연산 요소를 앞서 적는 표기법이다. x + y를 전위 표기법으로 바꾸어 작성한다면 + x y 가 될 것이다.
이렇게 리스트 자료구조를 활용한다면 대수식을 완성할 수 있을 것이다. 이제부터는 대수식 자체를 활용하면 되기에 이는 추상화 장벽을 구성하게 된다. 이후 대수식을 다룰 부분에서는 리스트 자료구조를 이용한 대수식 구현에 대한 자세한 서술이 필요없어진다.
이제 이전 유리수 파트에서 유리수를 pair 이라는 자료구조로 표현한 뒤, 사칙 연산을 구현했듯 미분도 그렇게 진행하면 된다.
아래는 대수식에 대한 도함수 연산의 종류이다.
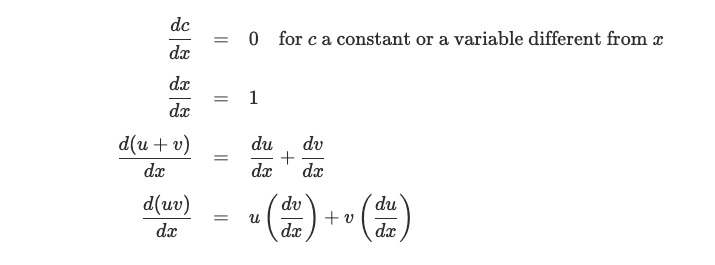
- 상수인 경우 미분하면 0이 된다.
- x는 x로 미분하면 1이다
- 두 대수식의 덧셈의 미분 결과는 각각을 미분한 결과와 동일하다.
- 두 대수식의 곱의 미분 결과는 각각을 미분한 결과와 동일하다.
이제 본격적으로 함수 요리를 만들기 전에 요리 재료부터 마련하자! 위 법칙을 만족하도록 미분하는 함수를 작성하기 위해 필요한 함수들은 다음과 같다.
| is_variable(e) | 변수 여부를 검사하는 함수이다. |
|---|---|
| is_same_variable(v1, v2) | 두 매개변수가 서로 같은 변수인지를 확인하는 함수이다. |
| is_sum(e) | 덧셈인지 확인하는 함수이다. |
| addend(e) | 합 e의 덧수를 의미한다. |
| augend(e) | Augend of the sum e. |
| make_sum(a1, a2) | Construct the sum of a1 and a2. |
| is_product(e) | Is e a product? |
| multiplier(e) | Multiplier of the product e. |
| multiplicand(e) | Multiplicand of the product e. |
| make_product(m1, m2) | Construct the product of m1 and m2 |
마무리
사실 이번 장의 내용은 유리수 파트와 상당히 비슷한 순서로 진행된다. 그리고 중간중간에 각 연산에 대한 비효율성을 줄일 수 있는 방법을 모색하고 각 연산의 구조를 개선하는 등 상당히 흥미롭게 진행된다.
이전의 유리수 파트를 꼼꼼히 읽었다보니 이 부분은 술술 읽히는 것 같아 기분이 좋다! 오늘도 알찬 내용! 수고했다 나 자신!