자바스크립트로 배우는 SICP - 13. 허프먼 부호화, 복소수와 제네릭 함수
허프만 부호화에 대해서 알아보자. 그리고 복소수를 추상화 해보자...! (사실 별개의 주제인데 겹쳤다는..?)
2023-11-06 | 독서 | 8min
오늘은 허프만 부호화 트리를 구성하는 방식에 관련된 내용을 읽었다. 보통 부호화는 다음과 같이 진행된다.
| A | 000 | C | 010 | E | 100 | G | 110 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| B | 001 | D | 011 | F | 101 | H | 111 |
즉, 각 이진 코드가 문자를 대표한다. 이를 이용하면, 이진수를 역으로 문자를 구성하여 해석할 수 있게 된다.(복호화 과정). 이러한 부호화 과정은 상당히 많은 컴퓨터 내 또는 컴퓨터 간 대화에서 이뤄진다.
문제는, 위의 예시를 보면 8개의 문자를 표현하기 위해 각 문자를 3자리 이진수로 표현했다. 이를 이용하여 문자열을 이진수로 바꿀 수 있다는 것은 사실이다. 그치만 더 공간을 효율적으로 활용할 수 있는 방법은 없을까? 있다!
위처럼 3자리 이진수로 통일하는 것이 아니다. 여기서 트리를 이용한다. 아래 그림을 보자.
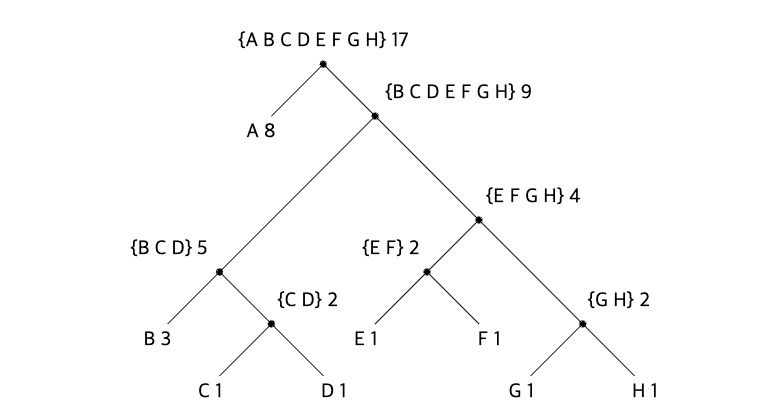
위 그림은 허프만 부호화 트리를 나타낸 것이다. 갑자기 트리라니 이게 무슨 말일까?
위의 트리의 잎 노드들을 보면 각 문자가 적혀있다. 그리고 각 문자에 도달하는 경로는 모두 다르다는 점을 이용하면, 왼쪽 가지를 이용할 때 0을, 오른쪽 가지를 이용할 때 1을 문자열에 추가하는 것이다. 이렇게 되면 앞서 작성했던 표가 아래와 같이 재작성될 수 있다.
| A | 0 | C | 1010 | E | 1100 | G | 1110 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| B | 100 | D | 1011 | F | 1101 | H | 1111 |
어라? 모든 문자들의 이진수 자릿수가 동일했던 이전과는 다르게 유동적이다. 역으로 복호화가 필요할 경우, 주어진 이진수들을 차례대로 이용하여 트리를 순회하고 잎노드를 찾아 반환하는 방식을 이용할 수 있다. 그럼 이게 어떤 이득을 줄까? 직접 예시를 보자!
부호화할 문자열: BACADAEAFABBAAAGAH
아스키 코드 방식: 001000010000011000100000101000001001000000000110000111
허프만 부호화 방식: 100010100101101100011010100100000111001111위 예시를 보았을 때, 허프만 부호화의 방식이 훨씬 공간을 적게 차지한다는 사실을 알 수 있다.
하지만, 만약 주어진 문자열이 H로 가득찬 문자열이라고 하자. 과연 허프만 방식이 더 효율적일까? 그건 아니다. 왜냐하면, 기존의 아스키는 3자리를 차지하지만 허프만의 경우 4자리를 차지하기 때문이다! 여기서 중요한 점은 어떻게 트리를 만들 것인가이다! 만약 트리의 균형이 무너져 한쪽으로 쏠리면 해당 문자를 많이 이용하는 경우는 문제가 될 수 있다.
그럼 이런 상황에서는 어떻게 벗어날까? 바로 문자가 얼마나 빈번하게 사용되는지에 따라 트리를 구성하면 된다. 빈번하게 사용되는 문자일수록 트리의 상단 즉, 그리 깊지 않은 곳에 배치하면 공간 효율성 면에서 매우 좋을 것이다. 대신 사용 빈도가 낮은 문자들을 더욱 깊이 배치하면 될 것이다. 이를 만드는 방식이 아래 그림과 같다.
| Initial leaves | {{(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)}} |
|---|---|
| Merge | {{(A 8) (B 3) ({{C D}} 2) (E 1) (F 1) (G 1) (H 1)}} |
| Merge | {{(A 8) (B 3) ({{C D}} 2) ({{E F}} 2) (G 1) (H 1)}} |
| Merge | {{(A 8) (B 3) ({{C D}} 2) ({{E F}} 2) ({{G H}} 2)}} |
| Merge | {{(A 8) (B 3) ({{C D}} 2) ({{E F G H}} 4)}} |
| Merge | {{(A 8) ({{B C D}} 5) ({{E F G H}} 4)}} |
| Merge | {{(A 8) ({{B C D E F G H}} 9)}} |
| Final merge | {{({{A B C D E F G H}} 17)}} |
첫 단계를 보면, 모든 문자들의 빈도수와 문자가 튜플로 나열된 형식을 확인할 수 있다. 여기서 각 단계가 진행될수록, 빈도수가 낮은 것들을 중심으로 튜플들이 조합되는 모습을 확인할 수 있다. 그리고 이 과정들이 반복되면서 모든 문자들이 합쳐질 때까지 진행되는 모습을 확인할 수 있다.
그리고 책에서는 위의 과정을 통해 트리를 구현하는 코드를 소개하고 있다!
이 다음으로는 추상 데이터를 표현하는 방법이 여러가지인 경우에 대해서 다루기 시작한다.
이전의 예시로 다뤘던 유리수에 대해서 표현하는 방식이 유일했다.(물론, 구현 상에서 그 차이는 날지 몰라도 유리수가 정수로 이루어진 분수의 형태로 표현될 수 있다는 사실은 자명하며 유일하다.)
하지만, 복소수의 경우 어떨까? 흔히 우리가 아는 복소수는 정수부와 실수부의 조합으로 이루어진다. 이는 곧 실수부와 허수부를 각 축으로 지니는 직교 좌표계 상에서 복소수를 하나의 점으로 인식할 수 있다. 그런데, 극 좌표계 또한 이용할 수 있다. 다음을 보자!
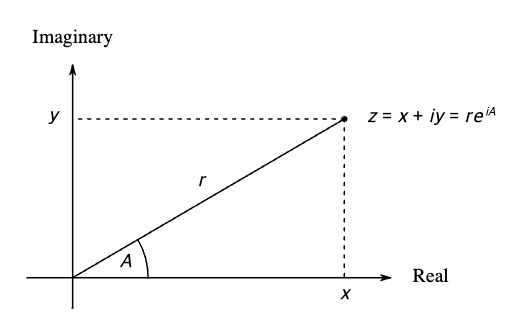
위 그림에서 볼 수 있듯 z 라는 복소수를 나타내기 위해서 라는 표현 방식도 유효하지만, 동시에 로 크기와 각도를 이용하여 복소수를 나타낸다.
이게 그러면 유리수와 차이점이 무엇일까? 실수, 허수부 표현은 말 그대로 이를 이용할 때, 실수나 허수 부분을 파악하기 용이할 것이다. 반대로, 극 좌표계를 이용한 방식은 크기를 파악하기 편할 것이다.
이는 복소수를 이용하는 프로그램들의 입장에서 각 연산에 용이한 방식을 선택하고 이용할 수 있게끔 추상화를 하는 것이 이 장의 목적이다. 아래 그림이 이를 소개하고 있다.
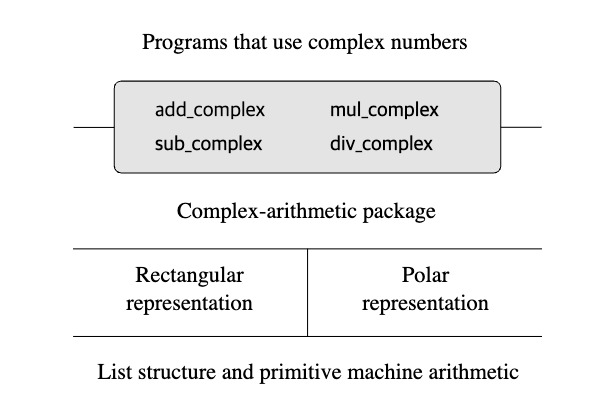
즉, 복소수를 표현하는데 두 방식이 가능하고, 복소수를 이용하는 프로그램들은 각 좌표계들에 모두 compatible 하도록 구현한다면 제대로된 추상화 장벽을 이용한다고 볼 수 있다.
이에 대해서, 책에서는 우선 복소수를 구현하는 함수를 만들고 각 좌표계 별로 연산 프로그램들을 다르게 구현한다! 여기까지가 오늘의 내용이다. 이후에는 프로그램별로 이 연산들을 구분할 수 있는 태깅하는 작업에 대한 내용을 제시한다!