자바스크립트로 배우는 SICP - 16. 다항식과 유리함수의 추상화

다항식을 추상화해보고 이를 이용해서 유리함수도 추상화해버리기!

2023-11-09 | 독서 | 10min

오늘은 데이터 추상화에 대한 예시로 다항식에 관련된 부분을 집중적으로 다룬다.

이전의 내용을 복기하자면, 수치 연산의 경우 정수의 사칙연산 → 유리수의 사칙연산 → 실수의 사칙연산 → 복소수의 사칙연산으로 조직화된 위계 구조가 있을 경우에 적용할 수 있는 추상화 전략(강제 형 변환)에 대해서 다뤘다.

이번 내용은 수치에 제한되지 않고 조금 더 일반적인 다항식의 경우에 대해서 다룬다. 보통 대수식의 경우, 피연산자들과 피연산자들 사이의 연산이 트리 형태로 조직화된 위계구조로 해석할 수 있다. 다음은 단순 예시이다.

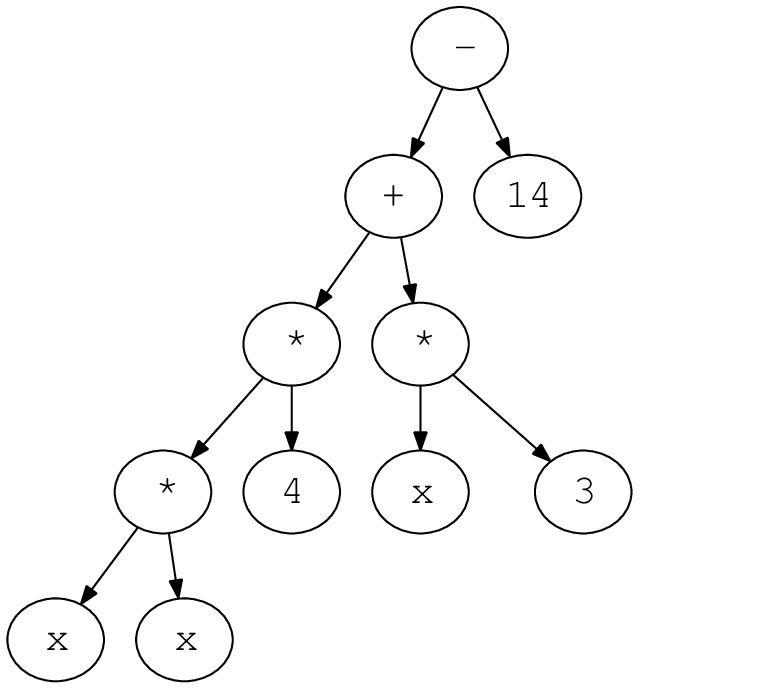
다항식 트리

책에서는 이러한 다양한 형태를 보일 수 있는 다항식을 구체적으로 정의하는 것을 우선으로 한다. 우선, 부정원 즉 미지수를 하나인 경우에만 다룬다고 제한을 둔다. (변수가 하나 = 일변량 다항식 = 일변수 다항식). 그리고, 보기 쉽게 곱셈과 덧셈만이 존재한다고 본다.

또한, 예를 들어 $5x^2+ 3x+1$ 이라는 식을 수학 함수로 인식하면 $5y^2+3y+1$ 와 다름이 없는 식이다. 하지만, 책에서는 이들을 구분적인, 키워드를 포함한 문장인 구문형 으로 간주하면 다르다는 것을 짚고 넘어간다.

이를 바탕으로 다항식의 덧셈을 구현하면 아래와 같이 작성할 수 있다.

function add_poly(p1, p2) {
    return is_same_variable(variable(p1), variable(p2))
           ? make_poly(variable(p1),
                       add_terms(term_list(p1), term_list(p2)))
           : error(list(p1, p2), "polys not in same var -- add_poly");
}

받은 두 변수가 다르다면 에러를 명시하면 된다.
변수가 같을 경우, 각 항들에 대해서 덧셈을 진행한 뒤 다시 polynomial로 구성하면 된다.

곱셈도 덧셈과 유사하다.

function mul_poly(p1, p2) {
    return is_same_variable(variable(p1), variable(p2))
           ? make_poly(variable(p1),
                       mul_terms(term_list(p1), term_list(p2)))
           : error(list(p1, p2), "polys not in same var -- mul_poly");
}

단순히 덧셈에서 항의 덧셈이 아닌 곱셈이라고 보면 된다.

그리고 이 함수들을 바탕으로 다항식 패키지 설치 함수를 구현하고 있다. (참고로 형태는 이전의 복소수에서 다뤘던 형태와 비슷하다. tag 함수로 태깅하고 put 함수로 테이블에 등록하는 방식을 이용한다).

여기에서 책에서는 더 구체적으로 들어가 add_terms 나 mul_terms 의 구현에 대해서 알아보고 있다. 이들은 모두 항 목록을 다루는 함수들로, 각각의 역할은 두 항 목록을 받아 곱셈 또는 덧셈을 진행하고, 만약 빈 항 목록일 경우 비어있지 않은 항 목록을 반환하도록 구현할 수 있다.

또 다른 관점으로, 항 목록을 표시하는 방법의 차이에 대해서 다룬다. 생각해보면, 항 목록을 위의 함수들을 구현할 때, 크게 신경쓰지 않았다. 단순하게 항의 선택자 또한 함수로 명명하고 아예 항 목록의 구현과 추상화 장벽을 세워버린다. 이는 이전에 다뤘던 내용의 반복으로 해석하면 좋을 것 같다.

다시 돌아와서, 항 목록을 표현하는 방법은 크게 두 가지로 나눌 수 있다. 다항식이 가깝거나 연속된 거듭제곱의 내림차순 형태로 구성되어있다면 단순히 각 항들의 계수를 list 자료구조로 나열한 방식을 이용하면 될 것이다. 그러면, 연속되지 않은 거듭제곱의 형태의 경우는 어떻게 다룰까?

앞선 방식은 비어있는 구간의 계수를 모두 0으로 표시한다. (예를 들면, $x^2+1$ 은 list(1,0,1) 이런 느낌이다. 문제는 $x^{100}+1$ 같은 경우를 표시하는 방법이다.) 이러한 방식을 적용하는 것은 공간을 낭비하게 만든다. 여기서는 항의 거듭제곱과 계수를 list 로 묶은 뒤, 이들의 조합으로 다시 항 목록을 구성하는 방식을 소개하고 있다. ( $x^{100}+1$ 의 경우라면 list(list(100, 1), list(0, 1)) 라는 방식을 이용한다는 것이다.)

이렇게 위에서는 다항식의 연산을 추상적으로 구현해보는 과정을 거쳐왔다. 다항식과 이전에 다뤘던 복소수의 차이점은 데이터의 타입 구조가 위계적이지 않다는 점이다. 그렇다면 서로 다른 타입의 다항식 간의 연산은 어떻게 진행할까? 이는 둘 중 하나의 타입에 맞게 다항식의 전개 순서를 변형시키면 된다. 물론 이는 변환 과정에서 다항식이 불필요하게 전개되거나 다루기에 비효율적이게 될 수 있다. (내 생각에는 상황에 따라 다르게 대응하는 것이 최선일 것 같다.)

추가로 다항식이 분자와 분모에 있는 유리함수를 다룬다. 그리고, 이 유리함수를 기약분수로 약분하기 위해 다음과 같은 과정을 소개하고 있다.

분자, 분모의 최대 공약수를 구한다. (다항식의 최대공약수를 구한다는 것이다. 이는 앞서 정수에서 다룬 유클리드 호제법의 방법을 그대로 이용하면 된다. 자세한 수학 내용은 여기(유클리드 환)를 참고하자.)
그리고, 분자와 분모의 차수 중 더 큰 값에서 최대공약수의 차수를 빼고 1을 더한 값만큼 부정원을 거듭제곱한 값을 위 아래에 곱하고, 최대공약수로 각각을 나눈다. (이 과정은 분자와 분모의 항들의 계수를 모두 정수로 만들어 다루기 쉽게 된다.)
마지막으로, 분자와 분모의 모든 정수 계수의 최대공약수를 구하여 이로 모든 계수를 나눈다.

이렇게 2장이 마무리 되었다. 사실 다항식과 유리함수의 부분은 상세하게 설명하고 있지는 않아 보였다. 사실 같은 과정을 이미 앞서 다뤘기에 그렇게 보인다. 게다가, 실제 상황과 어떻게 연관될까에 대한 궁금증이 아직 풀리지는 않았다. 그래서 내 생각에는 이 바로 전 장이 더욱 기억에 남았다. (사실 이 부분이 조금 어려웠기도 했다. 약간 책이 밥아저씨 같다. 이렇게 하면 됩니다~ 쉽죠..?😅). 쨋든 오늘도 수고했다!