자바스크립트로 배우는 SICP - 8. 쌍 객체 마개조 해버리기

쌍 객체를 알아보고 리스트를 구현해보자! 그리고 추상화는 덤!

2023-10-31 | 독서 | 10min

오늘은 쌍 객체에 대해서 다뤄볼 것이다! 그리고 쌍 객체를 이용하여 리스트 구조를 구현해볼 것이다! 그럼 키워드를 먼저 살펴보자.

키워드

오늘의 키워드는 다음과 같다.

• 쌍 객체와 닫힘 성질
• 순차열과 매핑

그럼 하나씩 키워드 중심으로 살펴보자!

쌍 객체란…?

쌍 객체란 무엇일까? 쌍 객체는 간단히 말해 쌍 자료구조가 적용된 함수라고 할 수 있다!

그럼 그 함수의 형태는 어떻게 생겼을까? (사실 이는 저번 포스팅에서 다룬 유리수를 구현하기 위해 사용했던 pair 함수가 대표적인 예시이다.)

우선 쌍 객체를 생성하는 pair 함수는 다음과 같은 구조로 이루어져있다.

function pair(x, y) { return m => m(x, y);}

즉, 두 개의 인수를 받아 해당 인수들을 담은 복합 데이터 객체를 반환하는 (정확하게는 함수를 반환하는) 형태이다. 이렇게 두 인수를 받아 하나의 복합 데이터 객체를 생성하는 pair 함수를 생성자라고 지칭한다!

이렇게 생성된 복합 데이터에서 각 인수들을 빼오는 함수들은 어떻게 작성할 수 있을까? 다음 코드를 보자.

function head(z) { return z((p, q) => p); }
function tail(z) { return z((p, q) => q); }

위 코드의 두 함수 head 와 tail 은 쌍 객체를 받는다는 것에 집중하자. 각 함수의 매개변수로 쌍 객체를 넣는다면, head 의 경우 첫 인수를, tail 의 경우 두 번째 인수를 반환하게 된다. 이들은 곧 pair 에 의해 생성된 복합 데이터 객체의 요소들인 원시 데이터 객체들에 접근, 즉 선택할 수 있는 함수들에 포함된다. 이러한 함수들을 선택자 라고 지칭한다!

쌍 객체와 닫힘 성질

이처럼 쌍 객체는 복합 데이터 객체를 생성하는 데 사용할 수 있는 기본적인 접착제를 제공한다. (즉, 추상 데이터라는 가정과 그 구체적인 표현 사이에서 선택자, 생성자라는 인터페이스들이 접착제 역할을 한다는 것으로도 이해할 수 있다.) 이를 보기 쉽게 그림으로 나타내보자!

다음은 pair(1, 2) 가 생성하는 쌍을 상자-포인터 표기법이라는 방식으로 나타내면 다음과 같다.

조금 더 추가해볼까? 다음 예시들에 대한 그림을 보자!

• pair(pair(1, 2), pair(3, 4))

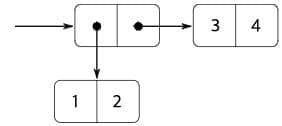
• pair(pair(1, pair(2, 3)), 4)

이제 조금 쌍에 대해서 익숙해졌을 것이다! 그리고 이러한 단순하지만 응용하기에 강력한 쌍을 잘 활용하면 타 자료구조들을 구현할 수 있겠다는 생각이 들 것이다…

다시 주제로 돌아와, 그럼 닫힘 성질과는 어떻게 연관되는 것일까?

우리가 수학에서 다루는 ‘닫힘’ 이라는 용어는, 어떤 집합과 연산이 있을 때 해당 집합의 원소들에 연산을 적용할 시 그 결과가 항상 해당 집합의 원소이면 해당 집합은 해당 연산에 대해서 닫혀있다고 정의한다. 이를 데이터 객체에 적용한 버전으로 생각하자면, 데이터 객체들을 조합하는 연산이 있을 때, 해당 연산으로 연산한 결과들을 다시 그 연산으로 조합할 수 있다면, 그 연산을 가리켜 닫힘성질을 충족한다고 말한다.

순차열, 넌 pair 손아귀에…

가장 간단한 쌍에 대해서 닫혀있는 자료구조 예시로는 순차열이 있다! 순차열은 유용하면서도 쌍을 활용한 목록 구조로 표현할 수 있는 강력한 닫힘 성질을 지는 자료구조이다!

그럼 아래 코드를 보자.

pair(1,
     pair(2,
          pair(3,
               pair(4, null))));

위의 위계적인 데이터는 아래와 같은 상자-포인터 도표로 나타낼 수 있다.

이러한 순차열을 나타낼 함수를 list 라고 해보자. 그러면 위 코드는 아래처럼 나타낼 수 있을 것이다.(단순히 예시일 뿐이지만 이와 같은 형태로 활용할 예정이다!)

const l = list(1, 2, 3, 4) // [1, [2, [3, [4, null]]]] 과 같은 구조를 반환할 것이다.

이러한 list 자료구조도 결국 pair 의 파생이기에 (pair 에 대해서 닫혀있기에) head 와 tail 이라는 함수를 적용할 수 있을 것이다.

head(l) // 1이다.
tail(l) // [2, [3, [4, null]]]이다. head를 제외한 나머지 부분이다.
head(tail(l)) // 2이다. 나머지 부분의 head에 속한다.

어라? 그럼 결국 pair 에서 적용하던 연산 방식을 list 끼리 적용할 수 있지 않을까? 당연하다! pair 에서 닫혀있기 때문이다. 아래 코드를 보자.

list(1, [2, 3], list(4, 5), 6) // [1, [[2, 3], [[4, [5, null]], [6, null]]]] 이다.

순차열 - n번째 요소 가져오기 (.at)

그럼 앞서 구현한 list 자료구조에서 n번째 요소를 얻어올 수 있는 방법이 있을까? (어떻게 보면, list 의 선택자라고 할 수도 있겠다.) 있다! 다음 코드를 보자.

function list_ref(items, n) {
	return n === 0
				 ? head(items)
				 : list_ref(tail(items), n - 1);
}
 
const squares = list(1, 4, 9, 16, 25);
 
list_ref(squares, 3);

위 코드의 list_ref 는 items이라는 list 자료구조의 n번째 요소를 반복적 과정을 통해 가져오는 방법이다. 간단하 소개하면, n이 0이 될때까지 반복적 과정을 거쳐 list_ref 를 호출해 0인 순간 head 를 선택하는 것이다.

순차열 - 길이 구하기 (.length)

그럼 순차열의 전체 길이도 구해보자!

function length(items) {
	function length_iter(a, count) {
		return is_null(a)
					 ? count
					 : length_iter(tail(a), count + 1);
	}
	return length_iter(items, 0);
}
 
const odds = list(1, 3, 5, 7);
 
length(odds);

length 라는 함수는 list 자료구조를 받아 전체 길이를 돌려준다! 함수의 구조는 어렵지 않다. 함수의 tail 요소가 null에 도달하기까지 반복적 과정을 거쳐 length_iter 라는 함수를 호출한다. 각 과정에서 is_null 함수를 통해 tail 이 null인지 그 여부를 검사한다.

순차열 - 뒤에 이어 붙이기 (.append)

추가로 순차열에 요소를 추가하는 append 함수에 대해서도 알아보자!

function append(list1, list2) {
	return is_null(list1)
				 ? list2
				 : pair(head(list1), append(tail(list1), list2));
}

위는 다음과 같은 과정으로 두 리스트를 이어붙인다.

1. 이어 붙일 대상이 되는 list1 의 head를 차례대로 추출하고 쌍을 구성한다.
2. 만약 list1 의 head를 모두 추출하여 더 이상 추출할 게 없다면 list2 를 반환한다.

이와 같은 과정들을 거치면, 두 리스트를 이을 수 있을 것이다.

매핑(자바스크립트의 map 그거 맞습니다)

이어서 순차열에 mapping하는 기능 또한 구현해보자!

순차열 - 각 요소에 n배하기

자바스크립트였다면, 배열.map(i ⇒ i*n) 처럼 구현했을 함수를 위 list 자료구조를 기반으로 구현해보자!

function scale_list(items, factor) {
  return is_null(items)
				 ? null
				 : pair(head(items) * factor, scale_list(tail(items), factor));
}
 
scale_list(list(1, 2, 3, 4, 5), 10); // [10, [20, [30, [40, [50, null]]]]]

위 함수는 list 자료구조를 받는 items라는 인수가 null이 아닐 때까지 items의 head 를 추출하고 배수를 적용하기 위한 인수인 factor 를 곱해서 나머지 tail 과 쌍을 구성하는 방식으로 작성되었다. 생각해보면 append에서 구현된 방식과 그리 다르지 않다. head를 하나씩 추출하고 그 head를 가지고 어떻게 지지고 볶고 하는 것이다. 🍲 … 🤨 어라 공통된 게 있네…? 추상화?

각 요소를 지지고 볶자 - map

공!통!패!턴! 그럼 바로 추상화다~! 앞서 말했지만 결국 list 에서 추출한 head 에 시즈닝을 뿌리는 방식은 똑같을 것이다. 이를 추상화하면 다음과 같이 구현할 수 있을 것이다.

function map(fn, items) {
	return is_null(items)
				 ? null
				 : pair(fn(head(items)), map(fun, tail(items)));
}

그럼 map 으로 구현한 scale_list는 다음과 같을 것이다!

function scale_list(items, factor) {
	return map(x => x * factor, items)
}

위 코드를 보면, 리스트에서 추출한 head에 값에 인수로 받은 fn 을 적용하고 있다! 이렇게 구성한 map 함수는 다음과 같은 이유들로 매우 중요한 함수이다.

1. 함수가 공통의 패턴을 포착한다! → 모듈화가 가능하다
2. 목록을 다루는 좀 더 높은 추상을 확립한다

여기서 집중해야되는 점은 바로 두 번째 이유이다. 앞서 구현한 scale_list 와 map 의 가장 큰 차이점은 무엇일까? 돌아가서 코드를 보면 “factor을 받아 리스트에서 head를 추출해 이를 곱하는” 과정이 모두 드러나 있다는 점이다. map 함수를 통해 구현한 scale_list 에서는 이 세부사항이 숨겨져 있으며 단순하게 각 요소에 factor 만큼 곱한다는 람다 표현식을 활용하기에, 목록의 요소들에 비례 변환을 적용해서 새 목록을 만든다는 고수준의 개념이 잘 드러난다. 이에 대해 책은 다음과 같이 이야기하고 있다.

… 두 정의의 차이는 컴퓨터가 서로 다른 과정을 수행한다는 것이 아니라(실제로는 같은 과정을 수행한다), 우리가 이 과정을 서로 다른 방식으로 생각하게 된다는 것이다. 본질적으로 map은 목록을 변환하는 함수의 구현과 목록의 요소들을 추출하고 조합하는 세부적인 방법 사이의 추상화 장벽을 세우는데 도움이 된다.

마무리

이렇게 오늘은 쌍 객체와 순차열 자료구조를 구현하면서 닫힘 성질과 추상화 장벽에 대해서 알아보았다. 매번 느끼지만 이 책은 정말 유익하다. 매번 나를 놀라게 하고 매번 도움이 된다. 매 장이 고트다. 🐐 

사실 책 부분은 162쪽부터 182쪽이라 트리 부분까지 포함되지만, 트리는 그 다음 내용과 연관성이 많아 끊어가고 싶지 않아서 제외했다. 아마 다음 파트의 처음에 등장할 것이다. 이 지식들을 곱씹어가며 다음 내용을 음미해보자~ (표현이 너무 독특한가…?)

쨋든 오늘도 알찼다! 수고했다 나 자신!